Dreiecke und Winkel
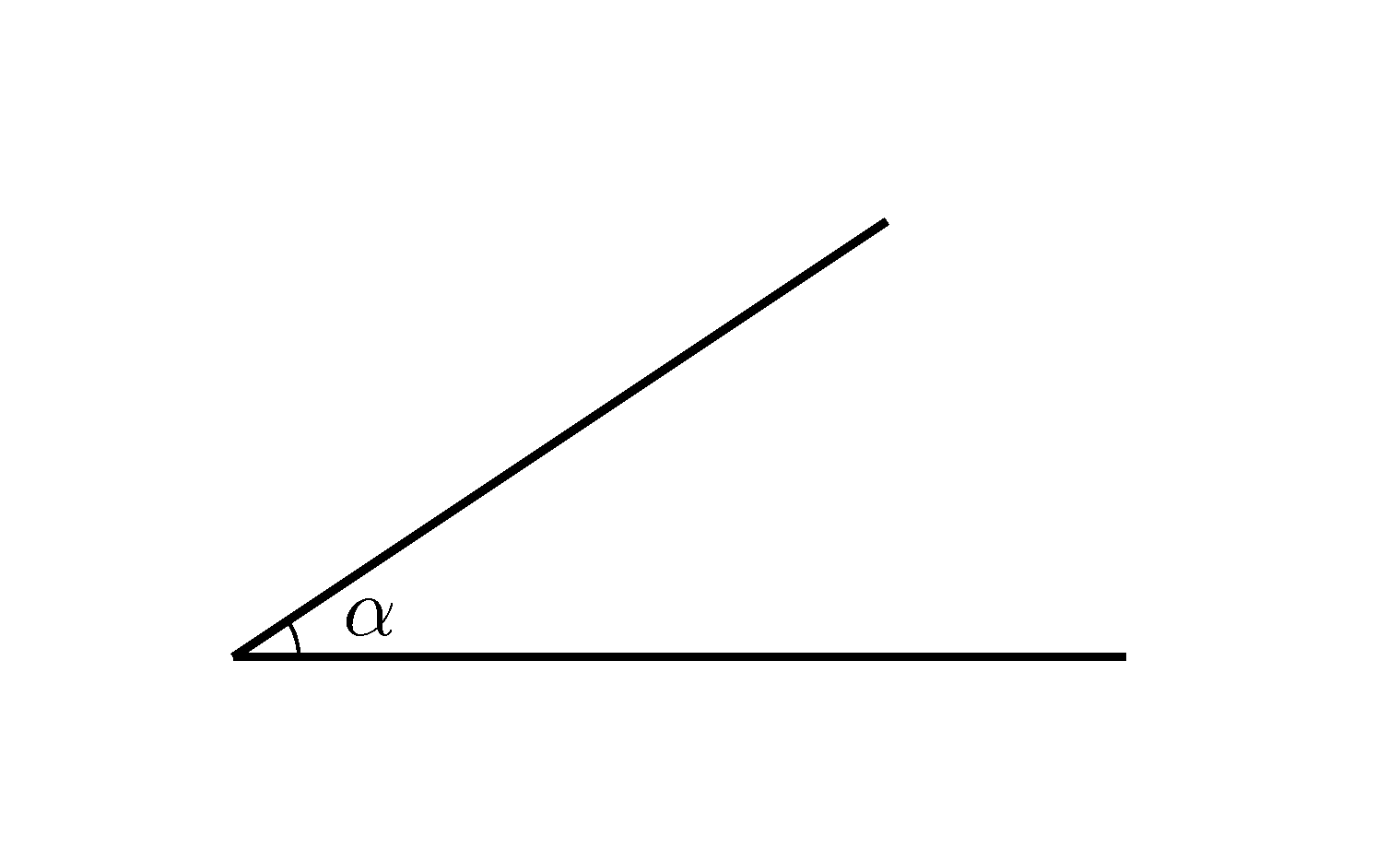
Ein Winkel wird durch zwei Halbgeraden festgelegt. Diese Halbgeraden nennt man Schenkel.
Der gemeinsame Anfangspunkt der Schenkel heißt Scheitel.
Ein Dreieck A B C wird durch drei Punkte A, B und C definiert, die nicht auf einer Geraden liegen.
Die Punkte A, B und C werden dann Ecken des Dreiecks genannt.
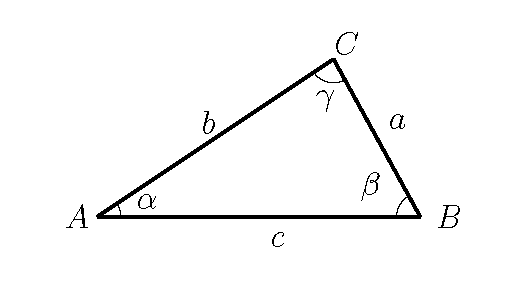
Die Strecke vom Punkt A zum Punkt B wird auch Seite genannt und mit c bezeichnet.
Man schreibt dann auch $\overline{AB}=c$.
Entsprechend heißt die Strecke $\overline{BC}$ auch Seite a und die Strecke $\overline{CA}$ Seite b.
$\alpha$, $\beta$ und $\gamma$ nennt man Innenwinkel.
Die Summe der Innenwinkel in einem Dreieck beträgt 180 $^\circ$.
$\alpha$ kann man in diesem Dreieck auch noch als Winkel B A C bezeichnen.
alpha gleich Winkel B A C
$\alpha = \measuredangle BAC$
Ein Winkel, der kleiner als 90$^\circ$ ist, heißt spitzer Winkel.
Ein Winkel, der größer als 90$^\circ$ und kleiner als 180$^\circ$ ist, heißt stumpfer Winkel.
Ein rechter Winkel ist genau 90$^\circ$ groß.
Wenn alle Seiten in einem Dreieck gleichlang sind, dann wird es gleichseitiges Dreieck genannt.
In einem gleichseitigen Dreieck sind die drei Innenwinkel gleichgroß. Sie betragen alle 60$^\circ$.
Besitzt ein Dreieck einen rechten Winkel, so heißt es rechtwinkliges Dreieck.
Ein gleichschenkliges Dreieck ist ein Dreieck, welches mindestens zwei gleichlange Seiten hat.
Beispiel:
Wenn die Seite a und die Seite b gleichlang sind, dann heißt das Dreieck gleichschenklig.
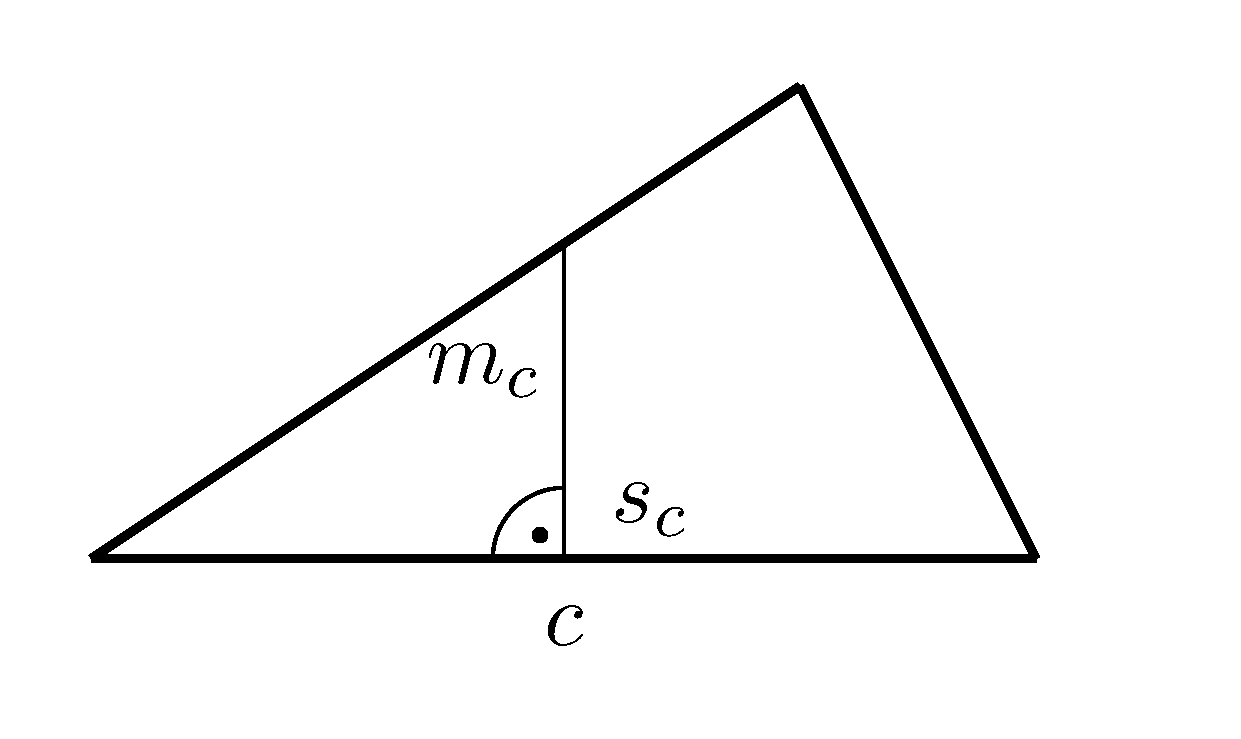
Die Seitenhalbierende $s_c$ verläuft von dem Eckpunkt C des Dreiecks durch die Mitte der gegenüberliegenden Seite c.
Die Mittelsenkrechte einer Seite c ($m_c$) verläuft durch den Mittelpunkt der Seite c und steht senkrecht auf dieser.
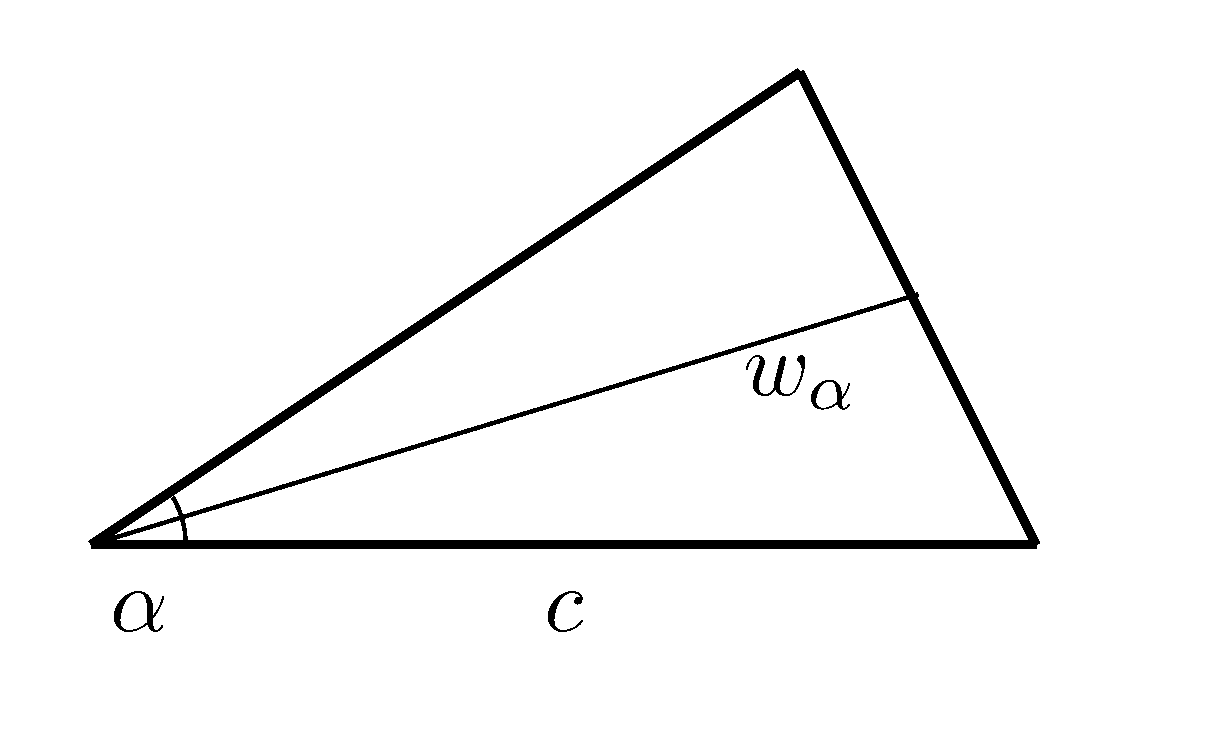
Die Winkelhalbierende eines Winkels Alpha ($w_{\alpha}$) teilt diesen Winkel in zwei gleich große Teile.