Vektorraum
Sei K ein Körper und M eine Menge. Weiterhin definieren wir $+\ : V \times V \to V \ ,\ (a,b) \mapsto a+b$ und $\cdot \: K \times V \,\ \to (\lambda, b) \mapsto \lambda \cdot b$.
Wenn alle nachfolgenden sieben Eigenschaften erfüllt sind, dann handelt es sich um einen K-Vektorraum.
1. Eigenschaft:
Für alle x, y, z aus V gilt in Klammern x plus y plus z gleich x plus in Klammern y plus z
$ \forall\ x, y, z \in V \ : \ (x+y)+z = x + (y+z)$
Die Verknüpfung 'plus' ist assoziativ.
2. Eigenschaft:
Für alle x, y, z aus V gilt in Klammern x plus y plus z gleich x plus in Klammern y plus z
$ \forall\ x, y \in V \ : \ x + y = y + x$
Die Verknüpfung 'plus' ist kommutativ
3. Eigenschaft:
Es existiert ein neutrales Element Null aus V, sodass für alle v aus V gilt: Null plus v gleich v plus Null gleich v
$\exists\ 0 \in V\ \forall \ \ v \in V \ : \ 0+ v = v + 0 = v$
o heißt dann neutrales Element bezüglich der Verknüpfung plus
4. Eigenschaft:
Für jedes v in V existiert ein minus v in V, sodass v plus minus v gleich minus v plus v gleich Null gilt
$ \forall\ v \in V\ \exists\ -v \in V \ : \ v + (-v) = -v + v = 0$
-v ist das inverse Element von v bezüglich der Verknüpfung 'plus'.
5. Eigenschaft:
Für alle lambda und mü aus K und für alle v aus V gilt: lambda mal in Klammern mü mal v gleich in Klammern lambda mü mal v
$ \forall\ \lambda, \mu \in K\ \forall\ v \in V \ : \ \lambda \cdot (\mu \cdot v) = (\lambda \mu) \cdot v$
Die Verknüpfung 'mal' ist assoziativ
6. Eigenschaft:
Sei 1 $\in$ K.
Für alle v aus V gilt eins mal v ist gleich v
$ \forall\ v \in V \ : \ 1 \cdot v = v $
7. Eigenschaft:
Für alle lambda aus K und für alle v, w aus V gilt lambda mal in Klammern v plus w gleich lambda mal v plus lambda mal w
$ \forall\ \lambda \in K\ \forall\ v, w \in V \ : \ \lambda \cdot (v+w) = \lambda \cdot v + \lambda \cdot w$
Es gilt also das Distributivgesetz.
Das Element v heißt Vektor.
Die Verknüpfung 'plus' heißt Vektoraddition.
Die Verknüpfung 'mal' heißt Skalarmultiplikation.
Sei K ein Körper und V ein K-Vektorraum. Seien weiterhin $v_1 \cdots v_k \in V$,$\lambda_i \in K$, $k \in \N$ und $i = 1, \cdots, k$.
Ein Vektor v aus V heißt Linearkombination von $v_1$ bis $v_k$, wenn es lambda aus K gibt mit:
v gleich die Summe von lambda i v i mit i gleich eins bis k
$ v = {\sum_{i=1}^{k} }\lambda_i v_i$
Eine Menge von Vektoren v eins bis v k heißt linear unabhängig, wenn gilt:
Aus Summe von lambda i v i mit i gleich eins bis k gleich null folgt lambda i gleich null für alle i
$ {\sum_{i=1}^{k}}\lambda_i v_i = 0 \Rightarrow \lambda_i = 0\ \ \forall\ i$
Eine Menge von Vektoren v eins bis v i heißt linear abhängig, falls sie nicht linear unabhängig ist.
Seien $a,b \in V$.
Vektorprodukt
Das Vektorprodukt der Vektoren a und b ist gleich a zwei b drei minus a drei b zwei , a drei b eins minus a eins b drei, a eins b zwei minus a zwei b eins
$\D a \times b =\begin{pmatrix} a_2 b_3 - a_3 b_2\\ a_3 b_1 - a_1 b_3\\ a_1b_2 - a_2 b_1 \end{pmatrix}$
Das Vektorprodukt nennt man auch Kreuzprodukt
Norm
$\Vert \cdot \Vert$
Sei $\Vert \cdot \Vert : V \to \R, x \mapsto \Vert x\Vert$ eine Abbildung. Diese Abbildung heißt Norm, wenn die folgenden drei Eigenschaften für alle $x,y \in K$ und für alle $\alpha \in K$ erfüllt sind:
1. Eigenschaft:
Die Norm von x ist größer als null, wobei x ungleich null ist: $ \Vert x\Vert > 0\ \ , x \ne 0$
Diese Eigenschaft nennt man Definitheit.
2. Eigenschaft:
Die Norm von alpha x ist gleich der Betrag von alpha mal die Norm von x
$ \Vert \alpha x\Vert = \vert \alpha\vert \cdot \Vert x\Vert$
Diese Eigenschaft nennt man auch Homogenität.
3. Eigenschaft:
Die Norm von x plus y ist kleiner gleich die Norm von x plus die Norm von y
$ \Vert x+y\Vert \le \Vert x\Vert + \Vert y\Vert$
Diese Eigenschaft nennt man auch Dreiecksungleichung.
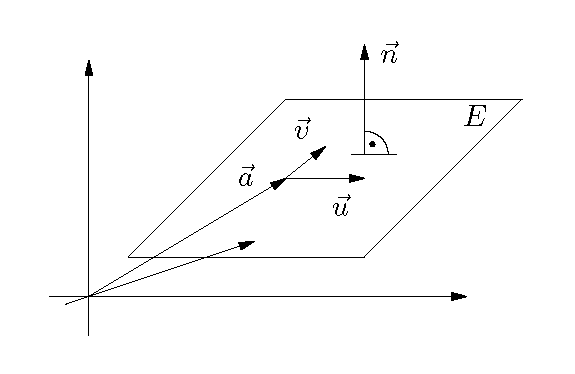
Wir betrachten nun im Folgenden das obige Bild.
Stützvektor
Ein Stützvektor a einer Ebene E ist ein Vektor, der vom Nullpunkt zu einem Punkt dieser Ebene zeigt.
Gerade
Seien $u, v \in V$ und $r \in K$.
x ist gleich u plus r mal v
$ x = u + r \cdot v$
Der Vektor v heißt Richtungsvektor.
Ebene
Seien p, u und v $\in$ V und $r,s \in K$.
x gleich p plus r mal u plus s mal v
$ x= p + r \cdot u+ s \cdot v$
p heißt Stützvektor.
u und v heißen Spannvektoren.
Ein Normalenvektor n steht orthogonal auf einer Ebene E.